- Published on
Phân tích giải thuật
- Authors

- Name
- ToanNV
Đặt vấn đề
Độ phức tạp thuật toán là một khái niệm quen thuộc với hầu hết các lập trình viên. Tuy nhiên, bạn đã bao giờ tự hỏi:
- Tại sao vòng lặp for có độ phức tạp ?
- Hai vòng lặp for lồng nhau thì có độ phức tạp ?
- Đoạn code này thì chạy mất bao lâu?
Thực ra thì ý niệm về thời gian chạy của công việc tính toán đã có từ rất lâu rồi, ít nhất là từ thời của Babbage. Ông từng nói:
Khi một máy phân tích xuất hiện, nó nhất định sẽ định hướng sự phát triển của khoa học trong tương lai. Mỗi khi một kết quả được tìm kiếm với sự hỗ trợ của nó, câu hỏi sẽ được đặt ra: Bằng cách tính toán nào mà máy tính có thể đạt được những kết quả này trong thời gian ngắn nhất?

Máy phân tích của Babbage có một cái tay quay. Khi ông quan tâm đến thời gian chạy của máy, thực ra ông muốn biết cần quay tay bao nhiêu lần để hoàn thành tính toán. Ngày nay, mặc dù cái tay quay đã được thay thế bằng các phép tính xảy ra hàng tỷ lần mỗi giây, nhưng mấu chốt vẫn là: chúng ta quan tâm đến việc cần thực hiện bao nhiêu thao tác rời rạc để hoàn thành một công việc tính toán.
Bằng những cách tiếp cận tương tự như vậy thì các nhà khoa học phát triển một phương pháp có tên là Scientific method để giải quyết vấn đề này. Scientific method bao gồm các bước cơ bản sau:
- Observe quan sát thời gian chạy chương trình.
- Hypothesize đưa ra một mô hình phù hợp với quan sát.
- Predict đưa ra các tiên đoán dựa trên giả thuyết.
- Verify kiểm chứng các tiên đoán đó bằng thực nghiệm.
- Validate lặp lại quá trình cho đến khi quan sát và giả thuyết có kết quả tương đồng.
Three-Sum
Hãy xem xét một ví dụ cụ thể: bài toán Three-Sum. Bài toán yêu cầu tìm số bộ ba số trong một danh sách sao cho tổng của chúng bằng 0.
Ví dụ với 8 số nguyên:
8
30 -40 -20 -10 40 0 10 5
Bằng mắt thường ta có thể thấy được có 4 bộ ba số có tổng bằng 0.
| a[i] | a[j] | a[k] | sum |
|---|---|---|---|
| 30 | -40 | 10 | 0 |
| 30 | -20 | -10 | 0 |
| -40 | 40 | 0 | 0 |
| -10 | 0 | 10 | 0 |
Mục tiêu là viết một chương trình tính số bộ ba đó cho một danh sách bất kỳ. Phương pháp đơn giản nhất là brute-force.
public int count(int[] a) {
int n = a.length;
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n; j++) {
for (int k = j+1; k < n; k++) {
if (a[i] + a[j] + a[k] == 0) {
count++;
}
}
}
}
return count;
}
Tiếp theo, chúng ta quan tâm đến thời gian chạy của hàm trên. Bạn có thể dùng đồng hồ bấm giờ, điện thoại hoặc một công cụ đo thời gian để thử nghiệm.
| n | time (seconds) |
|---|---|
| 250 | 0.0 |
| 500 | 0.0 |
| 1000 | 0.1 |
| 2000 | 0.8 |
| 4000 | 6.4 |
| 8000 | 51.1 |
| 16000 | ??? |
Dễ thấy rằng, mỗi khi tăng gấp đôi kích thước input, thời gian thực thi tăng lên đáng kể. Điều này có thể biểu diễn bằng một đồ thị với trục Y là thời gian chạy và trục X là kích thước input.
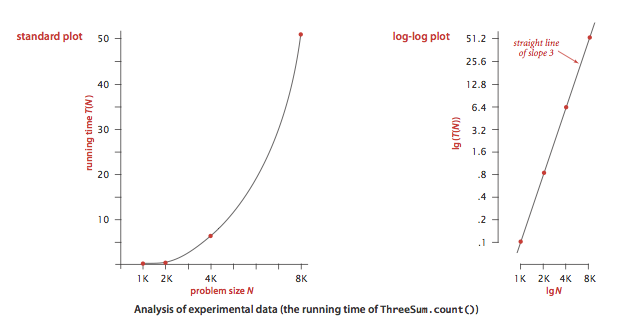
Để dễ dàng hơn trong việc phân tích, chúng ta vẽ đồ thị log-log. Trong biểu đồ này, đường thẳng có độ dốc bằng 3 cho thấy hàm thời gian chạy tỷ lệ với .
Thực ra, nếu áp dụng quy tắc hàm mũ (power law), bạn cũng sẽ có kết quả tương tự. Khi bạn có một đường thẳng với độ dốc , hàm của bạn sẽ tỷ lệ thuận với . Điều bạn cần làm là mỗi lần nhân đôi kích thước input và tính tỷ lệ thời gian chạy cho và . Tỷ lệ này sẽ hội tụ về một hằng số. Thực tế, log của tỷ lệ đó cũng hội tụ về một hằng số, và đó chính là số mũ của trong hàm thời gian chạy.
| n | time(seconds) | ratio | lg ratio |
|---|---|---|---|
| 250 | 0.0 | - | |
| 500 | 0.0 | 4.8 | 2.3 |
| 1000 | 0.1 | 6.9 | 2.8 |
| 2000 | 0.8 | 7.7 | 2.9 |
| 4000 | 6.4 | 8.0 | 3.0 |
| 8000 | 51.1 | 8.0 | 3.0 |
Vấn đề tiếp theo là ta cần ước lượng . Vậy làm thế nào để ước lượng ? Để xác định hằng số , chúng ta chỉ cần chạy thực nghiệm và giải phương trình.
Sau khi đã xác định số mũ , chúng ta có thể chạy thử nghiệm với giá trị lớn và so sánh kết quả với dự đoán từ mô hình đã vẽ đồ thị.
Từ giả thuyết này, chúng ta có thể dễ dàng dự đoán thời gian chạy cho các input 16000 và 32000.(Hãy thử ước lượng thời gian và kiểm chứng nhé)
Tuy nhiên, trong thực tế, có rất nhiều yếu tố ảnh hưởng đến thời gian chạy của chương trình. Các yếu tố độc lập với máy tính như thuật toán và dữ liệu bạn chạy là những yếu tố quyết định số mũ trong hàm mũ. Các yếu tố phụ thuộc vào hệ thống như phần cứng, phần mềm, và các chương trình đang chạy trên máy tính của bạn là những yếu tố quyết định hằng số trong hàm mũ.
Các mô hình toán học
Quan sát hiện tượng chỉ cho phép chúng ta tiên đoán hiệu năng, nhưng không giúp hiểu rõ thuật toán. Vì vậy, ta cần đến các mô hình toán học.
Khái niệm này được phát triển bởi Don Knuth vào cuối thập niên 60. Knuth đề xuất rằng chúng ta có thể tính tổng thời gian chạy của một chương trình bằng cách xác định các thao tác cơ bản, tính chi phí của chúng, và nhân với tần suất thực thi.
Ví dụ, với bài toán one-sum (tìm số lượng số bằng 0 trong một danh sách):
Như vậy là chỉ cần một vòng for, ta duyệt tuần tự và kiểm tra xem, nếu số đó bằng 0 thì sẽ tăng biến count.
int count = 0;
for (int i = 0; i < n; i++) {
if (a[i] == 0)
count++;
}
Phân tích đoạn code trên một chút. Chúng ta có:
- Có phép so sánh giữa với .
- Có phép so sánh giữa với 0.
- Có lần truy nhập mảng
Phân tích tương tự cho bài toán two-sum (tìm số lượng cặp số có tổng bằng 0):
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = i +1; j < n; j++) {
if (a[i] + a[j] == 0)
count++;
}
}
Trong đoạn code này, biến và được khởi tạo và gán giá trị lần. Số phép so sánh và truy cập mảng có thể tính toán dựa trên tần suất thực thi.
Phép so sánh bằng 0 có vẻ phức tạp hơn một chút. Ta có thể thấy rằng mỗi lần lệnh if chạy thì có hai lần truy cập mảng và một lần so sánh bằng 0. Vậy lệnh if được chạy bao nhiêu lần?
lần ở lần lặp thứ nhất,
lần ở lần lặp thứ 2,
và 0 lần ở lần lặp cuối cùng.
⇒ có phép if. Nghĩa là có lần truy nhập mảng, và phép so sánh bằng 0.
Tương tự như vậy, ta có thể tính được số phép so sánh nhỏ hơn là:
Số lần chạy phép ++ thì cũng không cố định, nhưng nó giao động trong khoảng từ đến .
Với những bài toán đơn giản như one-sum, two-sum thì chúng ta có thể dễ dàng thống kê được tần suất của các thao tác cơ bản. Tuy nhiên, với những bài toán phức tạp hơn, việc đếm các thao tác cơ bản sẽ trở nên khó khăn. Vậy câu hỏi đặt ra là: Có cần thiết phải đếm tất cả các thao tác cơ bản? Điều này tương tự như thống kê. Khi tập mẫu đủ lớn, không cần phải tính toán toàn bộ dữ liệu. Ở đây cũng vậy, khi ước lượng thô là đủ tốt thì không cần phải tính toán đầy đủ tất cả các phép toán cơ bản. Dĩ nhiên, bạn vẫn có thể đếm từng thao tác, đặt trọng số và cộng chúng lại. Nhưng thực tế, người ta chỉ cần đếm những thao tác chạy chậm nhất (có chi phí cao nhất hoặc được thực hiện nhiều lần nhất). Trong bài toán two-sum, thao tác được thực hiện nhiều nhất là truy cập mảng, với tần suất lần.
Ok, đến đây ta có , vậy nó nằm ở đâu?
Trong thực tế thì người ta sẽ làm thêm một bước đơn giản hóa mô hình toán học. Bước đó gọi là tilde notation. Tạm dịch là lấy xấp xỉ. Trong bước này ta sẽ bỏ qua các hệ số bậc thấp hơn trong công thức.
Tại sao lại vậy?
Vì hàm và có sự sai khác không quá lớn, nên chúng ta sẽ xét đến cặp hàm số: và
Với nhỏ thì ta có thế thấy sự khác biệt về giá trị của 2 hàm này tương đối lớn. Nhưng chúng ta không quan tâm đến nhỏ, vì chúng ta đang cần ước lượng thời gian chạy cho lớn. Khi nhỏ thì thời gian chạy cũng không đáng kể.
Khi lớn, giá trị của chúng dần tiến lại gần nhau. Khi đó, hay .
Quay lại với bài toán two-sum, khi này ta sẽ có . Như vậy, với mô hình chi phí và phép xấp xỉ, ta có thể ước lượng thời gian chạy của chương trình two-sum là với là hằng số.
Trong thực tế có rất nhiều cách tính xấp xỉ(cái này liên quan nhiều đến giải tích và toán rời rạc), nhưng người ta hay sử dụng Euler–Maclaurin formula. Khi đó thì ta có thể thừa nhận một số kết quả:
Hay ba vòng for lồng nhau như trong bài toán three-sum sấp xỉ với
Kết luận
Như Knuth đã nói, tồn tại các mô hình toán học chính xác cho thuật toán. Tuy nhiên, trong thực tế, các mô hình xấp xỉ đủ dùng để mô tả thời gian chạy. Đôi khi, chúng ta sử dụng toán học để chứng minh, nhưng đôi khi chỉ cần trích dẫn công trình của các chuyên gia.
Dự liệu test cho bài toán three-sum: 1K-ints 2K-ints 4K-ints 8K-ints 16K-ints 32K-ints 1M-ints Nguồn tham khảo: Analysis of Algorithms